Filters:
Kamehameha is now ruler of all the …
Years: 1796 - 1796
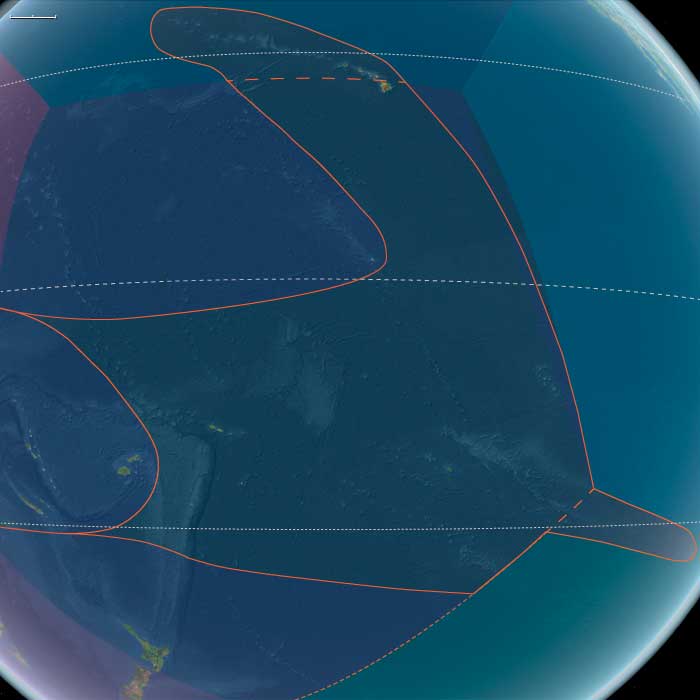
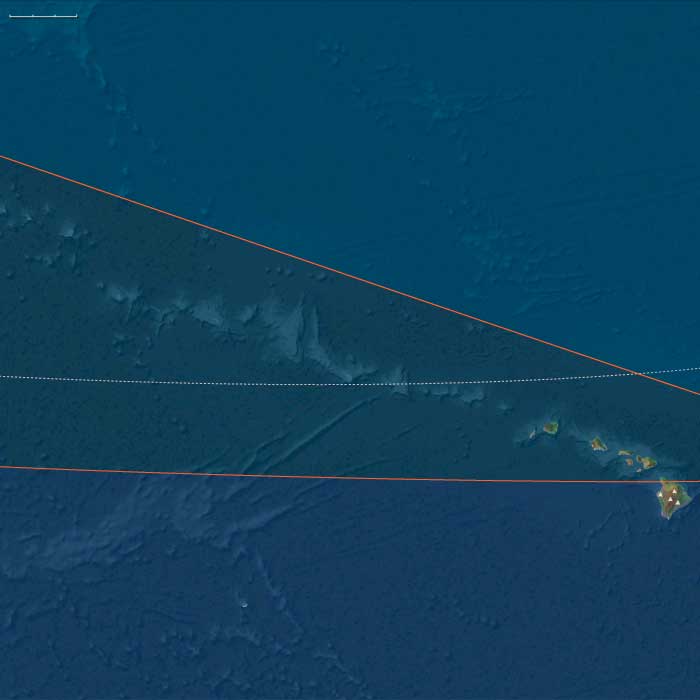
Kamehameha is now ruler of all the Hawaiian Islands from Oʻahu to the east, but the western islands of Kauaʻi and Niʻihau continue to elude him.
Using Honolulu as a base, he has a forty-ton ship built.
When he attempts to invade the western islands in 1796, Kaʻiana's brother Namakeha leads a rebellion on Hawaiʻi island against his rule, and Kamehameha is forced to return and put down the insurrection.
Locations
People
Groups
Topics
Commodoties
Subjects
Regions
Subregions
Years: 1796 - 1796
Locations
People
Groups
Topics
Commodoties
Subjects
Regions
Subregions